How to Divide on an Abacus with a Two Digit Divisor?
Now that we have learned Basic Division and Division with a Single Digit Divisor, let’s continue this time considering division with a 2 digit divisor. If you are new to abacus math or need a little refresher on addition and subtraction on the soroban, please take a look at some of the earlier lessons like Simple Addition and Subtraction on the Abacus. With a 2 digit divisor we must multiply both digits of the divisor by the quotient digit and subtract the resulting products from the dividend. In some cases we may find the initial quotient digit used for the first divisor digit may be too large for the second divisor digit forcing us to adjust the quotient digit value until the second divisor digit product is small enough to subtract from the dividend. In other words, sometimes our initial quotient digit guess may be too large. Here again is where Abacus Math really shows the benefits of this systematic approach to arithmetic. Instead of starting over and trying a new quotient value, we will show you a simple systematic way to adjust the current quotient digit until we find the correct value. In order to reduce the number of quotient adjustments needed to arrive at the correct quotient value, we will also learn a few simple rules for choosing our initial quotient digit so that statistically we are as close to the correct value as possible without over complicating the process.
To begin the abacus math division problem, place the dividend 1425 on the soroban and the divisor 19 with about 4 rods of separation.
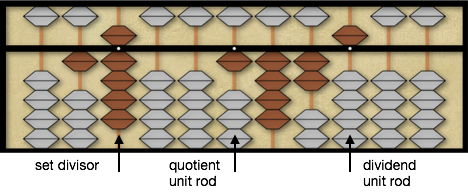
Notice the first digit of the divisor, 19, is the same as the first digit of the dividend 1425, where both are 1. Instead of dividing 1 into 1 we now compare the second digit of the divisor, 9, with the second digit of the dividend, 4, seeing 9 is larger than 4 respectively. When the second digit of the divisor is larger than second digit of the dividend the best quotient guess is 9. This is one of the simple rules we will follow to determine our initial quotient digit that will minimize the number of quotient adjustments we may need to make. So we place 9 as the first quotient digit on the quotient 2nd rod. The reason we place the 9 on the quotient 2nd rod is because our divisor 19 is larger than the first two digits of the dividend 14 so we need to move one more rod to the right on the quotient to enter our first digit.
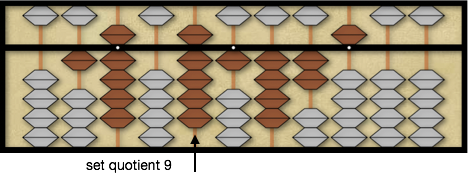
Since we are converting long division into a series of subtractions, we subtract 1×9=9 from the first two digits of the dividend, 14, leaving 525 as the remainder of the dividend.
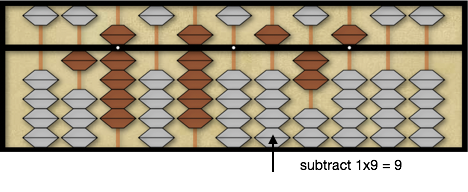
Next, we multiply the quotient 9 by the second divisor digit 9 for a product of 9×9=81 and compare 81 to 52 on the soroban. Since 81 is larger than 52, it means that the first quotient digit, 9, we chose is too large. Therefore we will follow a simple process to adjust our quotient digit to find the correct value. We do this by reducing the quotient digit 9 by 1 until we find a solution. Reducing the first quotient digit by 1, we must also return the product 1×1=1 back to the abacus from where it was subtracted. The reason we return 1 back to the abacus is because we had subtracted the first divisor digit 1 times the quotient digit 9 from the dividend. So when we adjust the quotient by 1, we have to return to the dividend 1 times the first divisor digit 1 or 1×1=1. Therefore, we reduce the quotient digit 9 by 1 to 8 and add 1×1=1 to 5 on the 3rd rod of the dividend. We now have a dividend of 625 on the abacus and a quotient digit 8.
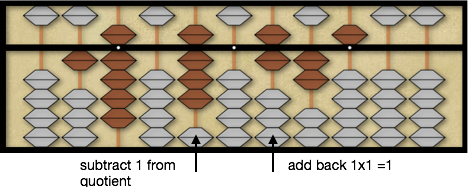
Repeat the same process by again comparing the second divisor digit, 9, times the new quotient digit 8, 9×8=72, to 62 on the soroban after adding the 1 back to the dividend. However, 72 is still larger than 62 on the dividend and the quotient digit is still too large. Again we subtract 1 from the quotient reducing 8 to 7 and adding back another 1×1=1 to the 6 on the abacus so we now have 725 on the dividend.
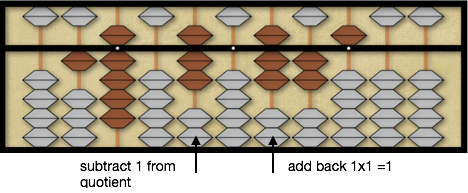
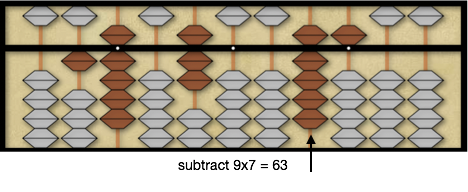
Now we compare the divisor 9 times the new quotient digit 7, 9×7=63, to 72 on the soroban. We can now subtract 63 from 72 leaving 95 on the soroban. First we subtract the 6 from 7 on the 3rd rod of the dividend. Next we subtract the 3 from 2 on the 2nd rod of the dividend by first subtracting 1 from 1 on the 3rd rod and adding 7, the 10 pair of 3, to 2 on the 2nd rod leaving 95 on the dividend.
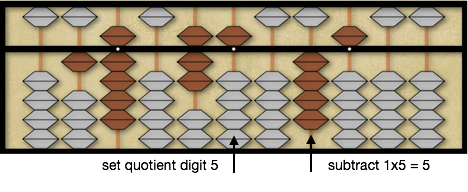
Next we compare the first divisor digit 1 to 9 on the soroban. If we were to place 9 as our second quotient digit we can easily see that multiplying the second divisor digit 9 times 9, 81, would be much larger than the 5 that would be remaining on the soroban. When divisor digit is 1 and the dividend digit is large, in this case 9, 5 is a good initial quotient guess. So we will place 5 as our second quotient digit and subtract 1×5=5 from the 9 on the soroban leaving a dividend of 45.
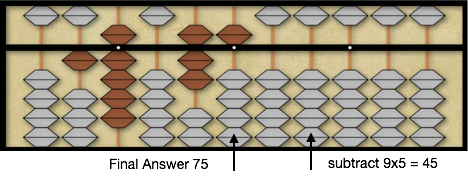
Finally subtract the product of the second divisor digit 9 times 5, 9×5=45, from the remaining 45 on the soroban clearing the dividend for a final answer of 75. In this example we got to see again how abacus math mechanizes the arithmetic process into a simple digit by digit calculation. We also learned two very useful rules for determining the initial quotient guess and how to adjust the quotient if the guess was too large. This is one of the areas where so many students feel long division is difficult trying to figure out what is a reasonable quotient guess. In the traditional method if the guess is wrong students typically start over. But in the abacus math method we mechanically home in on the correct quotient quickly with a process that continuously refines our initial guess one digit at a time. Using the abacus math method, students quickly begin to develop a deep sense of what quotient is likely to be correct increasing their math insights and understanding of long division.